大数の法則、中心極限定理、大偏差原理などの確率論における極限定理は、ランダムな現象における法則を記述するものとして、理論上、また物理学や工学、経済学などの応用上も重要な役割をはたしてきた。しかし、それらをめぐり解決されねばならない問題も数多い。特に大偏差原理については、それが成立するための良い十分条件も知られてこなかった。また、パラメーターnをふくむある無限次元空間上の汎関数の積分のnを無限大にとばす時の漸近挙動についてのBolthausenらの結果をより弱い条件に拡張することは、重要な問題である。また、それとは異なるタイプの無限次元空間上の汎関数の積分の漸近挙動を調べることも、ランダム行列の研究において要請されている。本論文において、これらの課題に対してひとつの解答を与える。 平均と分散が存在する実数値独立同分布な確率変数列にたいして、大数の法則(以下LLNと書く)がなりたつ。それにたいして、もとの変数の分布がすべての指数モーメントをもつという仮定のもとでは、大偏差原理(LDPと書く)がなりたつ。たんにLLNだけでなく、LDPがわかると、i.i.d.の平均のさまざまな汎関数の積分にたいして、その挙動をしらべることができる(Varadhanの定理)。以上の状況において、本論文では、次の問題に対して解答をあたえる。 (i)より弱い仮定で、無限次元化したレベルでの大偏差原理を示す。 (ii)Varadhanの定理を精密化する。 (iii)Varadhanの定理が使えない状況においてもi.i.d.の平均のさまざまな汎関数の積分にたいして、その精密な挙動をしらべる。 (i)の問題にたいする主結果は以下のとおりである。ポーランド空間X上の(右連続かつ左極限が存在する)道の空間 の元 の元 にたいし、時間2tごとに周期化したものを にたいし、時間2tごとに周期化したものを t,それを時間sだけshiftしたものを t,それを時間sだけshiftしたものを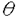 s s tと書く。 tと書く。 上の定常測度Pにたいして 上の定常測度Pにたいして  とおく。ここで は は 上のデルタ関数である。 上のデルタ関数である。 定理.定常過程Pがhypermixing propertyをみたすならば、定常過程の空間のすべての閉集合Fにたいして  またすべての開集合Gにたいして  がなりたつ。ただし、H(Q)はQのPにたいする相対エントロピーである。 つぎに、(ii)の問題にうつる。Xを実Banach空間とする。Varadhanの定理によれば、F∈Cb(X)、とすると、  にたいして 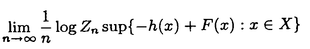 がなりたつ。ただしhはエントロピー関数である。Znの、これよりも精密なオーダーを調べることが、応用上も重要である。Bolthausenは,X上の汎関数J(x)=-h(x)十F(x)が最大値を一点のみでとる場合に、そのまわりでD2Jが退化を許す場合もこめて、上の問題の結果をあたえた。本論文では、Jの最小値をとる点の集合Vにたいして制約がない場合について、結果をあたえる。各x∈Vにたいして、Ax={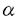 ∈X*:D2J(x)(a,a)=0}とする。結果はつぎのとおりである。 ∈X*:D2J(x)(a,a)=0}とする。結果はつぎのとおりである。 定理:Xに埋め込まれるd次元リーマン多様体Mで、V⊂M,各x∈VでAxTxM、M上の正値連続開数c,M上の非負値連続関数lでV上0であるようなものが存在して、  が成り立つ。ただし、J0はJの上限、 Mは、Mの体積要素である。 Mは、Mの体積要素である。 最後に、(iii)の問題を取り扱う。(ii)では、Varadhanの定理を基礎としてその上に理論が組み立てられたが、ここではそれを使えない場合を考える。以下、 とし、相互作用の関数V:E×E→Rにたいしては、以下の仮定をおく。 とし、相互作用の関数V:E×E→Rにたいしては、以下の仮定をおく。 (i)Vは対称、かつ ある0<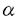 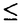 1にたいして、 1にたいして、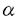 -ヘルダー連続。 -ヘルダー連続。 (ii)E上の確率測度の空間の上の汎関数J[ ]=∫V(s,t) ]=∫V(s,t) (ds) (ds) (dt)は、唯一の点 (dt)は、唯一の点 0で最小値をもつ 0で最小値をもつ (iii) 0はdtにたいして正の連続なRadon-Nikodym derivativeをもつ。 0はdtにたいして正の連続なRadon-Nikodym derivativeをもつ。 (iv)V0=V-J[ 0]とする。L2( 0]とする。L2( 0)上の作用素 0)上の作用素 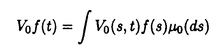 の固有値 k,K=1,2,…は、P< k,K=1,2,…は、P< をみたすあるpにたいして、 をみたすあるpにたいして、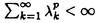 をみたす。 をみたす。 以上の仮定をみたすVにたいして、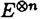 上の確率測定度Pnを 上の確率測定度Pnを  により定義する。Znは規格化定数である。このとき、以下の定理が成立する。 定理.  ただし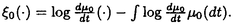 定理. なる なる にたいして にたいして  仮定をみたすVの一例は、十分な滑らかさをもち、かつ対称、周期1をもつR上の関数 にたいしてV(s,t)= にたいしてV(s,t)= (s-t)によってあたえられる。 (s-t)によってあたえられる。 |