集合E上の多変数関数からなる集合Cは,射影関数をすべて含み,合成に関して閉じているとき,E上のクローン(clone)とよばれる。E上のn変数関数の全体を,それらの和集合U_n>0をO_Eと表わし,E上のクローンの全体をL_Eと表わす。L_Eは(代数的に)束の構造をもつので,E上のクローン束とよばれる。とくにEが有限集合の場合を考察することが多い。Eがk個の要素からなる有限集合のとき,,O_E,L_Eを各々,O_k,L_k,と表わす。

　対象がブール関数の場合,すなわちk＝2のときのクローン束L₂の構造はすでに完全に解明されている。一方,k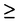3である各kに対してはL_kの構造は未だほとんどわかっていない。O_kに含まれる(真)部分クローンのうちで極大であるものを極大クローンというが,k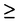3に対する既知の顕著な結果としては,わずかに,極大クローン全体の決定などをあげることができる程度である。なお,L₂の濃度は可算無限であるが,各k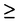3に対しL_kの濃度は連続濃度であることが知られている。

　本論文では,クローン束L_kの構造の解明,とくに,3値論理に対応するクローン束L₃の構造の解明を大目標として,いくつかの異なる視点から,構造の解明に資するための基礎的な研究を行った。

　本論文は4つの部分から構成される。

　第1部では,L₃に属するクローンのうち3値単調増加関数全体からなるクローンO(1)を考察の対象とし,O(1)に対する極大クローンをすべて決定した。O(1)自体はL₃における極大クローンの1つである。極大クローンの極大クローンを準極大(submaximal)クローンとよぶことがある。この用語を用いると,第1部の内容は,3値のクローン束においてO(1)に含まれるすべての準極大クローンの決定,と言い表すことができる。k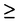3に対するクローン束L_kについて,準極大クローンを統一的に求めた結果は本研究以前には見当たらない。

　得られた結果は次の通りである。O(1)に含まれる準極大クローンは全部で13個存在する。それらのうち11個はO(1)と他の極大クローンとの積集合として得られるクローンであり,残りの2つは,関数maxと1変数単調増加関数の全体とから生成されるクローン,および,関数minと1変数単調増加関数の全体とから生成されるクローンである。

　第2部では,本質的極小クローンという概念を導入し,その分類に関する研究を行った。上に述べたように,極大クローンはすべて決定されているが,極大クローンの対極に位置する極小クローンについてはまだ散発的な結果しか得られてなく,極小クローンをすべて決定する問題は極めて困難な問題であるということが共通の認識となってきている。本論文では,L_kから1変数関数によって生成されるクローンをすべて取り除いて得られる半順序集合に着目し,その半順序集合における極小元を本質的極小クローン(essentially minimal clone)と名づけた。(技術的な理由により,本質的極小クローンの定義には,さらに,極小クローンではないという条件を付加している。)本質的極小クローンを考察する理由は主に次の2つである。1つは,関数合成の立場から見るとき,1変数関数によって生成されるクローンは例外的な存在であって,その意味で,考察の対象からはずすのが自然であると考えられることである。もう1つの理由は,極小クローンの場合その生成元fが2変数以上のときfのidempotent関数f(x,…,x)は常に恒等関数となるが,本質的極小クローンでは生成元fのidempotent関数は恒等関数ではないので,これが本質的極小クローンの決定にあたって有効な道具となりえて,極小クローンよりも状況が調べやすいことである。実際,本論文に示すように,現時点で,本質的極小クローンの研究は,極小クローンの研究よりもかなり先んじていると言うことができる。

　第2部(A)では,まず,本質的極小クローンの個数が各kに対して有限個であることを示した。次に,本質的極小クローンCの生成元をfとするとき,fをfのidempotent関数のサイクルの集合上に制限して得られる関数が本質的関数であるか否かによって本質的極小クローンをタイプ(I)(本質的関数である場合)とタイプ(II)(本質的関数でない場合)に分類した上で,タイプ(I)の本質的極小クローンについて研究し,その特徴づけを与える次の結果を得た。

　関数がタイプ(I)の本質的極小クローンの生成元であるための必要十分条作は,fが次の条件(i),(ii),(iii)をみたすことである。(ここで,fのidempotent関数をf^*とおき,f^*のサイクル上の要素の集合をAとおく。)

　(i)A⊂E

　(ii)f^*○f^*＝f^*であり,かつ,すべての(x₁,…,x_n)∈Eⁿに対し次が成り立つ。

　(iii)(a)f(Aⁿ)⊆Aであり,fをAⁿ上に制限して得られる関数はA上の極小クローンを生成する。または,(b)f^*(f(x₁,…,x_n))は本質的関数ではない。

　次に,第2部(B)では,タイプ(II)の本質的極小クローンのうち2変数関数によって生成されるクローンを対象として分類の研究を行った。2変数関数によって生成されるクローンはgroupoidとよばれる。主な結果は次の通りである。

　次の5つの組の各々について,与えられたすべての等式をみたす2変数関数fによって生成されるクローンはいずれもタイプ(II)の本質的極小クローンである。(ただし,簡単のためf(x₁,x₂)をx₁x₂と表わす。)

　(1)(xy)zx(xy)xy²xy

　(2)(xy)zx(y(xx²))xy,x(xy)xx²

　(3)x(yz)x²,(xy)²(xy)yx²yxy

　(4)(xy)zxy,x(yz)x(x²)

　(5)ある素数pと特定の要素0∈Eに対し,

　第2部(C)では,本質的極小クローンの大きさについて考察する。極小クローンと同様,本質的極小クローンはクローン束のなかの最下部の近傍に位置するクローンであり,含まれる関数の個数は比較的少ないものと予想される。実際,semilatticeに付随するjoinの演算で生成される極小クローンなどは,各n>0に対し,本質的n変数関数をちょうど1つしか含まない。しかし,本論文では,この予想が必ずしも正しくないことを,基礎の集合Eが無限集合の場合について示した。証明したのは次の結果である。自然数の集合N上の本質的極小クローンで,本質的2変数関数を可算無限個もつものが存在する。証明は,実際にそのようなクローンを構成することによって行った。

　第3部では,クローン束L_kにmetricを導入し,L_kを距離空間として考察した。L_k上の距離関数d_kは次のように定義される。クローンC₁,C₂∈L_kに対し,C₁＝C₂ならばd_k(C₁,C₂)＝0,C₁≠C₂ならば。本論文ではまず,L_kはコンパクト距離空間となることを示し,次に,クローンCが有限生成であることと孤立点であることとの関係を調べた。

　さらに,L_k上の連続写像について考察し,束のmeetの演算をもとにして連続写像を構成する方法を示した。とくにL₃からL₂への連続写像を2つ構成して,それらによるL₃の極大クローンの像やYanov-Muchnikのクローン族の像の分布の様子を調べた。この研究の動機は,既知の構造,すなわちL₂,と未知の構造L₃を連続写像を媒介にして結び付け,L₂に関する情報をもとにしてL₃の構造の解明を図ろうというものである。現時点では,この目標はまだ十分に達成されたとは言えないが,今後の更なるクローン理論の進展に向け,1つの新しい研究の方向を示したものと言えよう。

　最後に,第4部ではI.G.Rosenbergにより最近導入された超クローン(hyperclone)について考察を行った。集合E上の超クローンとは,E上で定義される多変数関数で値域がEのベキ集合であるような関数からなるクローンのことである。本論文では,集合{0,1}上の超クローン束の濃度は連続濃度であることを証明した。これはI.G.Rosenbergが提示した問いに肯定的な解答を与えたものである。なお,{0,1}上の超クローン束は,3値の通常のクローン束のなかのある半順序関係によって定まる部分クローン束に対応するものであり,ここで得られた結果は通常のクローン束L₃の構造の解析にも寄与するものである。

　論文の表題は

　The structure of the lattice of clones in multiple-valued logic

　(多値論理におけるクローン束の構造)

　である。ここで取り扱われている主題のcloneとはclosed set of logical functionsの略で、内容的には有限集合上の何個かの多変数関数の射影(projection)と合成(composition)で閉じている関数の族の成す束である。

　出発点となる有限集合はもとは、有限値の多値論理(multiple-valued logic)、計算機科学のスイッチング理論(swiching theory)や論理設計(logical design)を想定したものであったが、現在では関数族の極小生成系(minimal generatingfamily)や極小表現可能性(minimal representability)とも関連して、関数系の束としての構造の問題として代数的・位相的側面から研究が進められている。

　この分野の基礎概念の構築者としてはポスト(E.L.Post)、マルシェフ(A.I.Mal’cev)、ヤブロンスキー(S.V.Yablonskii)およびローゼンベルグ(I.G.Rosenberg)などが挙げられる。2元集合上のclone束についてはポストによって1941年に、その束としての(包含関係による)構造が完全に決定されている。その後、マルシェフによる諸概念の定義と基礎的部分の体系化の基礎の上に、ヤブロンスキーによって1958年に、3元集合上のclone束について、極大元の全体の構造が決定された。これらの結果や手法を拡張・発展させてローゼンベルグは1965年から1970年にかけて、任意有限集合上のclone束の極大元を完全に決定し、1970年代はこの分野の活発な発展の時代に導いた。

　n＝2のポストの結果はclone束の構造を、何個かの無限の系列を含めて、完全に決定したもので、最も簡単な場合とはいえ非常に優れた結果である。n＝3の場合においてさえ、上述のように極大元について完全な情報が得られたとはいえ、clone束の構造は非常に複雑で、任意の元での切断上の双対空間、例えば、おる元の下の元の極大元の全体、あるいはその順序を反転した対象物、などの構造はほとんど未知のまゝである。このことはヤノフ(I.Yu.Yanov)とムチニーク(A.A.Muchnik)によって1959年に、n＝2についてはclone束の基数(cardinality)は可算であるが、n>2についてはclone束の基数は連続体の基数(cardinality of continuum)をもつことが証明されていることからも解る。

　この論文で本論文提出者は、L_kをk上のcloneとして、次のような諸結果を導いている。

　1.L₃の単調関数の成す極大cloneの下の極大元(submaximal clone)の全体構造を決定した。submaximalな元については最初の結果であり、ラウ(D.Lau)は町田氏の1982年の結果を発展させて他のsubmaximal cloneの系列を得ている。しかし、L₃でさえすべてのsubmaximal cloneの全体構造の決定は将来の問題である。

　2.L_kの極小cloneについて、極小cloneの基本的性質と特徴づけ定理を導いた。特にL₃の極小cloneの何個かの例を構成した。また、essentially minimal cloneという概念を導入して、そのほとんど完全と思われる特徴づけ定理を証明した。この結果も本研究者の固有の着想が用いられている。

　3.L_kに距離の概念を導入し、L_kの距離空間(metric space)としてとらえ、cloneの間の連続関数の成す圏(category)の構造の研究を進めた。この概念の応用として、特にL₃からL₂への具体的連続関数を構成し、その微細構造の研究の基本的概念を導入した。

　4.ロゼンベルグ(I.G.Rosenberg)が1998年に提出した2元集合上のhyper cloneの全体集合が連続体の基数をもつか、という問題に肯定的解決を与えた。

　これらの研究成果は、極大cloneの全体像についてのみ比較的よく知られていた状況のなかで、submaximal cloneとかminimal cloneのように、町田氏によって初めて導入され、あるいは成された構成例や特徴づけ定理によって、本格的な研究の糸口が見つけられたものも多く、その創造性は高く評価されるべきものである。

　当研究分野は未だ発展の途中段階にあり多くの未解決の重要問題を含んでいる。町田氏は将来もこの方向の研究を継続し、本質的貢献を成す資質を有することは本論文はじめ、参考論文として既に8編の欧文研究誌の論文があることなどが示している。

　よって、論文提出者 町田元は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。