学位論文要旨
| No | 123860 | |
| 著者(漢字) | 伊藤,健一 | |
| 著者(英字) | ||
| 著者(カナ) | イトウ,ケンイチ | |
| 標題(和) | 散乱多様体上のSchr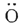 dinger方程式と超局所的特異性 dinger方程式と超局所的特異性 | |
| 標題(洋) | Schr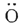 dinger equations on scattering manifolds and microlocal singularities dinger equations on scattering manifolds and microlocal singularities | |
| 報告番号 | 123860 | |
| 報告番号 | 甲23860 | |
| 学位授与日 | 2008.03.24 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第318号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | 数理科学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 本論文の内容は一部を除いて中村周教授(東京大学)との共同研究に基づいている. 目的は多様体上でのSchrodinger方程式の解の特異性について論じることである. 散乱多様体上のSchrodinger作用素 散乱多様体とはMelrose(1994)により導入された非コンパクト多様体の一クラスであり,散乱理論を多様体上で展開する際に有効とされている.Riemann多様体(M,gsc)が散乱多様体であるとは次で定義される: 1,多様体Mに対して分解M=MoM∞;Mo∈M,M∞(0,∞)×∂Mが存在する.ただし∂Mはある閉多様体とする.(無限遠方における.Mの位相的境界に対応する.) 2.M∞の遠方(r→∞,(T,θ)∈(0,00)x∂M)で計量gscが錘型計量gcn=dr2+γ2gjk∂dθkに近づく.ここでg∂は∂M上のRiemann計量である. Rnにおける極座標の拡張であることに注意する:Rn={X<1}∪((0,∞)×sn-1).このときMの無限遠方が漸近的Euclid空間の構造を持つものと解釈される.我々はこの散乱多様体上でLaplace-Beltrami作用素を用いたSchrodinger作用素H=-△sc+Vを考える.ただしポテンシャルVは滑らかであり,遠方ではv(<2)次多項式以下の増大度をもつとする. 超局所的平滑化作用 以上の条件の下で時間推進作用素e-itHの特異性を調べる.波動関数の波面集合は,古典的には,運動量無限大の成分に対応する.一方,e-itHの波動関数への作用は,相空間で見た場合,対応する古典系の時間発展となる.(誤差を含む.)従って,波動関数の特異性の解析は,古典系における運動量無限大の粒子の運動の解析に対応する.(cf.伝播速度無限大)この視点に依れば,初期状態における波面集合型の特異性は非零時間では遠方での波動関数の増大に移される.そして,また,この逆も成立するため,時間推進作用素による平滑化作用が期待される. 自由なHamiltonian K=Σj,kgsc(jk)ξjξkに対するHamilton方程式の解を(x(t),ξ(t))=exptHK(xo,ξo)とする」→±∞で軌道が有界領域に留まるとき(xo,ξo)は捕捉的であると言い,そのような点の集合をT±とする.計算により,初期データがT*M\T±に属するなら,極限(ρ±,θ±,ω±)=limt→±∞(ρ(t),θ(t),ω(t))が存在することが分かる.ただしは(γ,θ)∈M∞から誘導されるT*M∞=T*(0,∞)×T*∂Mの局所座標を(r,ρ,θ,ω)とする. 定義(斉次波面集合)超関数u∈S'(M)と(ro,ρo,θo,ωo)∈T*M∞に対し(ro,ρo,θo,ωo)¢WFhg(u)〓定理1 古典系ではv<2のとき運動量無限大でポテンシャルの影響が無視されることに注意する.これは中村教授(2005)のEuclid空間における結果の多様体上への拡張である.非零時間における波動関数の位置一運動量の各成分は,初期状態のそれを陪特性曲線に沿って伝播させたものとなっていおり,運動量無限大の成分は,無限遠方からも伝播速度無限大で伝わってくる.従って初期データuがある超局所的方向に強い減衰を持っていれば瞬間以降/以前にその方向から来る情報を集めてもそれは大きくはならない,よって波面集合となって現れない,ということを意味している。 この方面ではCraig-Kappeler-Strauss(1995)の超局所平滑化作用(以下,CKS)が知られているが,定理1はCKSの仮定における減衰方向を超局所解析的な意味で局所化した結果,結論も時間に関して局所化されることを意味しており,CKSの精密化になっている. Wunsch(1999)はEuclid空間(Rn,dz2)上での自由時間推進作用素の積分表示において積分核に二次振動が現れることに着目した.散乱多様体上では無限遠での構造が一様に規定されているため,関数uの遠方における一次振動e±λrを定量することができ,散乱波面集合WFsc(u)として捉えることが出来る(Melrose,1994).Wunschは,同様にして,二次振動を捉える方法として,二次散乱波面集合WFqsc(u)(⊂T*M∞)を導入し,その伝播を完全に調べた. ところが,次の定理により二次散乱波面集合は斉次波面集合と同値であることが示される. 定理2任意の超関数u∈S'(M)に対して,Wunschは無限遠で減少するポテンシャルを扱ったが,斉次波面集合の方法を用いると,ポテンシャルの増大度に関する仮定はv<2(subquadratic)にまで弱めることができる.2次以上の増大を持つポテンシャルに対しては異なる性質の伝播が既に知られているため,定理2に注意すると,定理1はWunschの結果の一部を最良のポテンシャルにまで拡張したものになっていることが分かる. 時間推進作用素の特異性の特徴付け ポテンシャルにより強い仮定v<1を与えると散乱理論の方法を用いることで,定理1を更に精密化することが出来る.散乱理論を適用するためには適当な比較系を設定する必要があるが,我々は多様体Mfr=R×∂M上の作用素Hfr=-∂r2を用いる.計算により古典的逆散乱作用素が存在することが分かる:〓ただしKfr(r,ρ,θ,ω)=ρ2をT*Mfr,上の自由なHamiltonia,Jc1*M∞→(0,∞)×∂M⊂Mfrは自然な同一視とする.またTfr±={±ρ≦0}とする.ω±*は時間±∞における古典散乱データである. 定理3v<1とする.±to>0に対して〓更にT±=T-=0(零切断)のときe(-itoH)J(eitoHfr)(±to>0)は次数0のFourier積分作用素であり,付随する正準関係は〓である. 系(xo,ξo)∈T*M\T,±to>0とする.このとき(Xo,ξo)∈WF(e(-itoH)u)⇔w*(xo,ξo)∈WF(e(-itoHfr)J*u).(1) (1)の右辺はuから簡単に求めることが出来ることに注意する.実際,一次元の自由時間推進作用素e(-itHfr)は具体的に書くことができ,更に前述の相空間での古典軌道(r,ρ)→(r+2tρ,ρ)との対応関係も剰余項無しでexactに書き下せるからである. 中村教授(2003)は漸近的Euclid空間において既に定理3の前半部分と同様の結果を得ているが,比較系が異なるため,単純な拡張一制限の関係にはない.また定理3はHassell-Wunsch(2005)による先行結果にも類似しているが,我々のアイデアおよび手法はより自然で簡潔である. 波動作用素の特異性 Jを(0,∞)×∂M⊃MfrからM∞への滑らかなcutoffと自然な同一視の合成とする.v<-1のとき波動作用素HJ-JH(fr)はH(fr)に対して相対コンパクトではないが,波動作用素〓が存在し,完全性が成り立っ. 定理4v<-1とすると〓更にT+=T-=0を仮定すると,W±は次数0のFourier積分作用素であり,付随する正準関係は〓である.同様の手法を用いることで散乱作用素S=W+W_のFourier変換S=Fr0s0*に対しても以下の結論が得られる.〓とすると,古典的散乱作用素は〓で与えられる.ここでκ∂(θ,ω)=Σjkg∂(jk)(θ)wjwkは∂M上の自由なHamil-tonianである.定理5v<-1とする.このとき原点近くで1をとる関数X∈0∞(R)に対して,〓はo次のFourier積分作用素で付随する正準関係は〓である.Melrose-Zworski(1996)は散乱行列が0次Fourier積分作用素で,あることを示したが,これはその一表現と考えることが出来る. | |
| 審査要旨 | 学位申請論文:Schroedinger euqations on scattering manifolds and microlocal singularitiesにおいて、伊藤氏は散乱多様体と呼ばれる、漸近的に錐状の計量を持っ多様体上のシュレディンガー方程式の解の超局所的性質、および散乱作用素の超局所的性質について考察している。シュレディンガー方程式の解は、特異性に関する有限伝播性を持たないため、解の超局所的性質を記述するには、波動方程式の場合と異なり、古典軌道の長時間の挙動を考慮する必要がある。この論文においては、比較系となる柱状の多様体とその上の力学系を適切に設定することにより古典力学的散乱理論を構成し、比較系の時間発展を用いて修正された時間発展の作用素が、古典的波動作用素の正準変換に対応するフーリエ積分作用素であることを証明した。この結果は、HassellとWunschによる既知の結果よりはるかに簡明な定式化であるとともに、拡張になっている。シュレディンガー方程式の解の時間無限大での漸近挙動を調べるには、修正された発展作用素の時間無限大の極限である波動作用素を考察するのが有効である。この論文においては、新しいアプローチによる波動作用素の定式化を導入し、有限の時間発展と同様の超局所的性質が成り立つことを証明した。さらに、この波動作用素は散乱波面集合に対応するシンボルクラスにおけるフーリエ積分作用素であることも証明した。 これらの結果は、優れた数学的業績であり、大きな学問的貢献であると評価できる。よって、論文提出者伊藤健一は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク |