学位論文要旨
| No | 118423 | |
| 著者(漢字) | 鈴木,香織 | |
| 著者(英字) | ||
| 著者(カナ) | スズキ,カオリ | |
| 標題(和) | Fano指数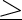 2の3次元Q-Fano多様体について 2の3次元Q-Fano多様体について | |
| 標題(洋) | On Q-Fano 3-folds with Fano index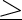 2 2 | |
| 報告番号 | 118423 | |
| 報告番号 | 甲18423 | |
| 学位授与日 | 2003.03.28 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数第223号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | 数理科学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 本論文の目的はピカール数が1でQ-分解的な3次元Q-Fano多様体の分類についての考察を行うことである.また,log del Pezzo曲面のカスケードと呼ばれる反射影の列を用いた例の構成を行う.その応用として,与えられたFano指数が2であって重み付き射影空間に低い余次元で埋め込まれる3次元Q-Fano多様体から高い余次元で埋め込まれる3次元Q-Fano多様体へのカスケードが構成できる. 定義.Q-Fano多様体とは,正規Q-Gorenstein射影多様体で高々末端特異点のみを持ち,かつ反標準因子が豊富となるものである.このようなFano多様体Xに対しFano指数を線形同値-Kx=fAを満たすWeil因子Aが存在する最大の正整数で定義する. 非特異Fano多様体の分類は1980年代までにIskovskikh,Mori,Mukaiらによって完全になされている.他方,MMP(Mori Minimal Model Programme)においてはQ-分解的な端末特異点を持つ多様体を扱うことが不可欠である.従って,このような特異点を持つ3次元Fano多様体の分類が次の重要な問題となる. 3次元多様体の分類に用いられる手法は筆者の知る限り大きく分けて三つある.一つはMMPの手法,二番目はMukai独自の手法で,これにより,非分解的なFano指数1の場合の分類が完成した.三番目が次数環を用いたReid,Cortiらによる手法である. Fano多様体の幾何学的な構造は,Fano指数によって大きく異なる.Fano指数が1という条件は,特にMMPを分類の手法とした場合には自然な流れではあるが,その分類は一般的には未解決であり,現在も活発に研究が進められている.一方,次数環を用いた手法では指数の値に関わらずFano多様体の構造が理解できるという利点がある.そこで本論文では上記の次数環を用いた手法でFano指数が2以上のQ-Fano多様体を取り扱う.Fano指数が大きくなることを用いて反標準因子-Kxではなく,比較的シンプルなAに付随する次数環を用いてQ-Fano多様体を多項式環の言葉で書き表すことができる.そのHilbert多項式を考えることにより具体的な有理多項式の計算からQ-Fano多様体について以下に述べる新たな知見を得た. 前半で示した定理は次の通りである. 定理1.XをC上の3次元Q-Fano多様体とし,ピカール数を1とする.この時,XのFano指数f=f(X)について次が成立する. (1)maxf(X)=19,f(P(3,4,5,7))=19. (2)もしf(X)=19ならば,XのHilbert多項式はP(3,4,5,7)のHilbert多項式と一致し,その値は1/(1-t3)(1-t4)(1-t5)(1-t7)である. (3)f∈{1,...,10,11,13,17,19}. 注意.(3)についてはf=10の場合を除いて全て存在が確認されている. 証明は次の[K]の定理を用い,Magma([Ma])というコンピュータープログラムを用いた計算によってなされる. 定理2(川又).XをC上の3次元Q-Fano多様体とし,ピカール数を1とする. εでΩ1xVVを表わす, (1)もしεがμ-半安定ならば,〓. (2)もしεがμ-半安定でないならば,Fをεのmaximal destabilizing sheaf,sをFの階数とし,tを〓を満たす正の有理数とする.この時次の不等式が成立: (a)S=1ならば,〓. (b)S=2ならば,〓. 注意.実際の論文では具体的な数値は明示されていないが,証明を読むことで上のような表示を持つことがわかる. 更に〓の場合に全ての特異点の組をbasketの意味で記述し,そのHilbert多項式及び反標準囚子の三乗の値と共に明示した.〓の場合もAに付随する次数環により得られる重み付き射影空間の埋め込みとしての余次元が2以下の場合についても同様のリストを作成した.また,次の結果を得た. 定理3.XをC上の3次元Q-Fano多様体とし,ピカール数を1とする.更に重み付き射影空間の中の埋め込みとしての余次元が3となるものは次の通り: (1)f=2ならばXは〓-型特異点を唯一持つQ-Fano多様体であり,-K3X=56/3,XのHilbert多項式は1+2t2-2t3-t5/(1-t)3(1-t3). これはP(13,22,3)のcoordinates x1,x2,x3,y1,y2,zを用いた5×5 skew matrixのPfaffianによって定義される3次元Q-Fano多様体のHilbert多項式と一致する.ここで各bijは2次同次多項式S(2)(x1,x2,x3,y1,y2)の元. (2)〓ならば重み付き射影空間の中の埋め込みとして考えた時の余次元が3となるものは存在しない. 注意.上のPfaffianはBuchsbaum-Eisenbudにより定義されたものである.[BE] 後半ではdel Pezzo曲面Tの〓点以下のblow upについて考察を行い特に次の定理を示した. 定理4.Tを商特異点〓を唯一つ持ち,-KT=OT(A)によってpolarizeされるdel Pezzo曲面とする.〓に対し,σ:T(d)→TをTのd個のgeneral points P1,...,Pdにおけるd点blow upとする.Eiで各Piたちの例外曲線を表わす.このとき (1)T(d)は〓-型の特異点を唯一つ持つlog del Pezzo曲面であって〓. (2)〓ならば,T(d)の次数環は次数1が7-d個,2が2個,3,4,5が各1個ずつの計12-d個の生成元を持ち,埋め込みT(d)⊂P(17-d,22,3,4,5)を与える.これは例外曲線Eiを次のdisjointな射影的正規有理曲線に移す: (3)T(6)の次数環は次数1,2,3,4,5各1個を生成元として持ち,T(6)を完全交差T6,8⊂P(1,2,3,4,5)の形に埋め込む.この埋め込み写像は例外曲線EiをT6,8内のdisjointな(-1)-curveに移す. 注意.A(d)=σ*A-ΣEiとする.この時,次数環R(T(d),-A(d))⊂R(T(d-1),A(d-1))はTypeI反射影によって与えられる.これは,次数1の生成元を新たに加えることで得られる. 同様に他のdel Pezzo曲面Tのblow upを考え,重み付き射影空間への埋め込みの余次元の高いdel Pezzo曲面から低いdel Pezzo曲面への射影による構成できる.今の定理でT(6)は余次元2の良く知られた構造をもち,これから出発することで,余次元の高いdel Pezzo曲面としてT,T(1),T(2),...,T(5)の構造の知見が可能になった. 得られた結果の応用として,Fano指数が2の3次元Q-Fano多様体についても同様の結果を得ることができる.del Pezzo曲面はその特異点〓達がa+1または〓modrかつHilbert多項式の1次の項の係数が1以上の時にFano指数が2の3次元Q-Fano多様体へ次数1の生成元を加えることで拡張可能である. このような例として前述の余次元3のQ-Fano多様体が挙げられる. 定理5.Tとして商特異点〓を唯一の特異点として持つ重み付き射影空間P(1,1,3)で,-KT=OT(A)によってpolarizeされるdel Pezzo曲面とする.〓に対し,σ:T(d)→TをTのd個のgeneral points P1,...,Pdにおけるd点blow upとする.Eiで各Piたちの例外曲線を表わす.このとき (1)T(d)は〓-型の特異点を唯一持つlog del Pezzo曲面であって(-KT(d))2=1/3+8-d. (2)T(6)の次数環は次数1,1,1,2,2,3各1個を生成元として持ち,T(6)をBucksbaum-Eisenbud Pfaffianを用いてTPf⊂P(13,22,3)の形に埋め込む. 上の定理のT(6)の反射影として得られた3次元Q-Fano多様体が定理3(1)で求めるものになっている. 謝辞:Miles Reid先生とは有意義な議論を交わし,また絶えず励ましの言葉を頂きました.ここに深く感謝いたします.Fano多様体に関して助言を頂きました宮岡洋一先生,高木寛通さん,そしてMagmaのプログラミングを教えて下さったGavin Brownさんに心より御礼申し上げます.最後に指導教官として温かく見守り,この論文に対し貴重な意見を下さいました小木曽啓示先生に感謝いたします. 参考文献 [BE]D.Buchsbaum,D.Eisenbud,Algebra Structures for Finite Free Resolutions,and Some Structure Theorems for Ideals of Codimension 3,Amer.J.Math.99(1977),447-485 [K]Y.Kawamata,Boundedness of Q-Fano Threefolds,Contemp.Math.131(1992),439-445. [Ma]Magma(John Cannon's computer algebra system):W.Bosma,J.Cannon and C.Playoust,The Magma algebra system I:The user Language,J.Symb.Comp.24(1997)235-265. | |
| 審査要旨 | Q-分解的な末端特異点のみを許し、反標準因子が豊富かつPicard数が1である正規射影代数多様体をQ-Fano多様体という。3次元Q-Fano多様体は、森、川又、Reidらによって確立されたいわゆる3次元極小モデル理論(森理論)において中心的な役割をはたす多様体の類の1つであり、その名の由来であるFano以来多くの人によって様々な立場から研究されている多様体の類でもある。 さて、Q-Fano多様体に付随する基本的な不変量に、Gorenstein指数r(X)とFano指数f(X)がある。前者は、Xの反標準因子-KXは何倍したらCartier因子になるかをあらわす最小の正整数であり、後者は-KXが数値的Weil因子類群(XのWeil因子全体のなす群を数値的同値類で割って得られる群)の中でどれだけ割れるかをあらわす最大の整数である。Fano指数がf(X)であれば、その定義から、-KX≡f(X)AXとなるWeil因子AX-ここではXの原始的Weil因子と呼ぶ-が数値的同値を除いて一意に決まる。 論文提出者鈴木香織は、3次元Q-Fano多様体を主にそのFano指数と次数環の観点から研究した。より具体的には、次の定理(博士論文における主定理)を得た。 定理.F:={1,2,…,9,10,11,13,17,19}とする。Xを3次元Q-Fano多様体、f(X)をXのFano指数、AXをXの原始的Weil因子とする。このとき、 (1)f(X)∈F. (2)3次元Q-Fano多様体P:=P(3,4,5,7)のFano指数は19である。更にf(X)=19ならば、(X,Ax)に付随するHilbert多項式と(P,Ap)に付随するHilbert多項式は一致する: (3)逆にf∈Fかつf≠10である整数fに対して、f(X)=fである3次元Q-Fano多様体Xが存在する。 この定理は、Q-Fano多様体のFano指数の有界性予想(Batyrevの予想)の3次元版の肯定的解決であるのみならず、(2)で保証されるように最良の評価を与えたという点でも意義深くかつ決定的なものである。 証明は特異Riemann-Rockの定理や川又氏による3次元Q-Fano多様体の有界性定理とその証明方法といった伝統的手法とともに、最後の詰めにおいてはマグマとよばれる次数環の計算に関するcomputer programをも使う新鮮なものである。 このように、論文提出者鈴木香織は、代数幾何学における興味あるテーマに取り組み、よい成果をあげた。 よって、論文提出者鈴木香織は博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク |