学位論文要旨
| No | 123869 | |
| 著者(漢字) | 手塚,勝貴 | |
| 著者(英字) | ||
| 著者(カナ) | テヅカ,カツキ | |
| 標題(和) | 既約な複素対称空間におけるSL(2,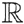 ) の固有な作用 ) の固有な作用 | |
| 標題(洋) | Proper Actions of SL(2,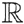 ) on Irreducible Complex Symmetric Spaces ) on Irreducible Complex Symmetric Spaces | |
| 報告番号 | 123869 | |
| 報告番号 | 甲23869 | |
| 学位授与日 | 2008.03.24 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第327号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | 数理科学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 1序 博士論文では、フックス群やクライン群のようなやや大きい離散群を基本群とするような局所対称空間がどの位存在するかをテーマとする。リーマン幾何の枠組みを超えた場合 局所対称空胃の基本群にはどの様な制約があるか?, という問題は非常に困難な問題である[8,13]。 無限位数の基本群をもつ完備な局所対称空間が存在するための必要十分条件は1989年に小林によって解明された[4]。 一方、コンパクト形の存在問題、すなわち余コンパクトな不連続群が存在するかどうかという問題は、リーマン対称空間に対しては1950年代から1960年代初頭にSiegel、Borelによって代数群を用いた手法で肯定的に解決され、非リーマン対称空間に対しては小林、Zimmer、Nlargulisによって、不連続群論からエルゴード理論やユニタリ表現論にまたがる手法を用いた新しい研究の潮流が生まれている[1,6,7,10,11,12,15]。 博士論文では、この中間に相当するフックス群やクライン群の非リーマン対称空間(特に複素対称空間)への不連続な作用に絞って研究を行った。 まずは、知られている事を復習しよう。 Gを半単純リー群として、HをGにおいて簡約な閉部分群とする。特に興味深いのは、Hがコンパクトでない場合である。その時、Killing形式から導かれる(G/H上の擬リーマン計量を考えると、GはG/Hに等長に作用する。半単純対称空間が古典的な例である。 rをGの離散部分群としよう。その時、rは擬リーマン多様体G/Hの等長変換から成る離散部分群と見なせるがrは必ずしも不連続群として作用する訳ではない。実際、G/Hの無限不連続群が存在しないという現象は最初、E.CalabiとL.Markus(1962)によって、正の定曲率を持つローレンツ対称空間で発見され[2]、カラビ・マルクス現象と呼ばれている。小林(1989)により、その必要十分条件が一般に解明された[4】。 Fact1.1.(カラビ・マルクス現象の必要十分条件[4];)簡約型等質空間に対する次の2つの条件は同値である。 (1)G/Hに無限不連続群が存在する。 (2)rankRG>rankGH. (2)⇒(1)の証明が非自明であり、それは(2)⇒条件S⇒(1)の形で示されている。ここで条件Sは次の形で述べられる。 条件S:Gの半単純元γで、Γ:=〈γ〉がG/Hに固有不連続に作用するものが存在する。 博士論文では、条件Sのかわりに 条件N:Gのべキ零元γで、Γ:=〈γ〉がG/Hに固有不連続に作用するものが存在する。 が、どの様な等質空間に対して成り立つかを考察した。 条件1Vでは一見、可換自由群ZのG/Hへの作用だけを考えている様に思われるが、実はSL(2,Z)の様な非可換な離散群の作用の固有不連続性も考えている事になる(定理A)。これを連続化した条件SLがいつ成り立つかも同時に考察する。 条件SL:SL(2,R)と局所同型なσの部分LでG/Hに固有に作用するものが存在する。 博士論文では、まず次の定理を証明した。 定理A.条件N⇔条件SL 定理Aで述べた同値な条件が成り立つ様な等質空間G/Hに対しては、SL(2,R)の任意の離散部分群(例えばSL(2,/Z))がG/Hに固有不連続に作用する。 博士論文では、定理Aで述べた同値な条件が具体的にどの様な等質空間に対して成り立つかを追及した。 2複素半単純対称空間Gc/KCにおける不連続群 この節ではG/Hを複素半単純対称空闇Gc/Kcとする。ここでGcは複素単純リー群、Kcは複素解析的な包合的自己同型写像θの固定部分群とする。リー環レベルでは、(s(n,C),so(n,C))などの7つの古典型の系列と、(¢6¢,テ4,c)の様な例外型の系列が12個ある。この場合の主結果は次の様に述べる事が出来る。 定理B.既約な複素対称空間Gc/κcが条件1V(あるいは同値な条件SL)を満たすための必要十分条件は、となる事である。ただし、p、qは奇数で、p+qは4の倍数。 Gcが複素リー群の場合には、条件SLは 条件SLR:3.L(2,(C)と局所同型な部分群LでGc/Kcに固有に作用するものが存在する。 とも同値となる。よって定理Bの系として次の結果も得られる。 系2.1.p、qは奇数、p+qが4の倍数の時、任意のクライン群rに対し、局所複素対称空間Mであって、その基本群π1(M)がrと同型であり、その普遍被覆空間がSpin(p+q,C)/Spin(p,C)×Spin(q,C)と同型なものが存在する。 証明の方針をここで述べる。 定理Aは、ベキ零元の標準化に関するJacobson-Morozovの定理と、作用の固有性に関する小林の判定条件[4]を用いる。定理Bの証明には次の結果を援用する。 定理C.9cを単純リー環とする。この時、次の2条件は同値となる。 (i)9cの外部自己同型写像は各ベキ零軌道を自分自身に写す。 (ii)9cは50(4n,c)と同型でない。 定理CはDynkin-Kostant理論を用いて {ベキ零軌道}→{重み付きDynkin図形} の同一視を行い、分類を用いて重み付きDynkin図形の外部自己同型に関する対称性を調べて証明を行った。 外部自己同型が不連続群の問題に現れる理由の一つはFact1.1(Calabi-Markus現象の判定条件)を用いて証明される次の結果で説明される。 命題2.2.Gc/Kcに無限不連続群が存在するならば、θは9cの外部自己同型である。特に、9cはAn、Dn、E6のいずれかである。 この命題2.2、定理Cと、固有な作用の判定条件を組み合わせる事によって、定理Bが証明されるのである。 コンパクトなCiifFord-Klein形が存在するかどうかに関して知られている結果と定理Bを比較してみよう。以下では〓を局所同型の意味で用いる。 Fact2.3.Gc/Kc輪は群多様体ではない既約複素対称空間とする。 (1)(小林1992、Beηo観1996)Gc/Kcに余コンパクトな不連続群が存在するならば、Gc/Kc〓S0(4n,C)/SO(4n-1,C)。 (2)(小林一吉野2005)σc/κc魁θ0(8,(C)/SO(7,C)には余コンパクトな不連続群が存在する。 SO(4n,C)/S0(4n-1,C)(n≧3)に対して余コンパクトな不連続群が存在するかどうかについては未解決問題である。一方、系2.1でp=4n-1、q=1とする事によりSL(2,C)の任意の離散部分群と同型な不連続群は存在する事が分かる。 3SL(n,R)の等質空間における不連続群 博士論文では、複素対称空間の場合だけではなく、実半単純リー群SL(n,R)が推移的に作用する種々の等質空間(半単純対称空間全て、及び非対称ではあるが1990年以降にZimmer、Labourie、Benoist、Mgzes、Margulis等、著名な数学者達が特に余コンパクトな不連続群の存在問題をテーマにして取り上げた例)に対して条件N、条件SLが成り立っための必要十分条件を決定した。この要約では3つの例に絞って説明しよう。 なお、論文[14]ではここに挙げた例以外の等質空間に対しても判定条・件を与えた。 定理D.(G,H)を(SL(n,R),SL(k,R))(k<n)とする。その時条件N(条件SL)が成り立つ必要十分条件は、nが偶数、またはnが奇数でん+1<nが成り立っている事である。 これは対称空間ではない典型例である。まず、小林(1990,1992)がn>塾+32の場合、SL(n,飛)/3五佛,飛)にコンパクトなClifford-Klein形が存在しない事を証明した([7,Example 5.19])。また、小林の定理の別証明としてn>2kの場合にはZimmer、Labourier、Mozes等はエルゴード理論やRatnerの軌道閉包定理を用いる手法(1994-1996)を開発した[10,11,151。一方、Benoist(1996)はη=hしない事を証明した国。この条件はSL(2,R)の固有な作用が存在しない条件に一致している事が定理Dより分かる。 次に対称空間と非対称空間を両方含む例を述べる。 定理E.(G;H)を(SL(n,R),30(p,q))p+q≦nとする。条件N(条件SL)が成り立つ必要十分条件は、n-2min(p,q)≧2である。 p+q=nの場合はG/Hは対称空間である。p+q<nあるいはp=qならば、SL(n,R)/SO(p,q)にはコンパクトなClifford-Klein形が存在レない事が知られている[7]。特に、SL(n,R)/SO(p,q)(p+q<n-1)には余コンパクトな不連続群は存在しないが、SL(2,Z)と同型な不連続群は存在する事が分かる。 最後に、HとLの役割を交換した定理を述べる。定理Fの等質空間を取り上げた直接の理由は、同じ空間に対してMargulis(1997)がユニタリ表現論を用いて、n>4の場合、余コンパクトな不連続群が存在しない事を証明したからである[12]。. 定理F.ρ:SL(2,R)→SL(n,R)を既約な実表現とする。 SL(n,飛)の(標準的〉部分群Lに対し,LがSL(n,R)/ρ(SL(2,R))に固有に作用するかどうかは、以下の表で与えられる。 | |
| 審査要旨 | 本論文提出者の手塚勝貴氏は、フックス群やクライン群のような双曲群が局所対称空間の基本群として現れるか、という問題を研究した。 一般に 問題A.完備な局所対称空間Xの基本群π1(X)にはどの様な制約があるか? という問題はリーマン幾何の枠組みを超えた場合非常に困難である。 その一例として、Xがアファイン平坦な局所対称空問の場合を考えてみる。Milnor(1977)はリーマン幾何における古典的な結果(Bieberbach1911)と同様に、アファイン平坦な場合でも基本群π1(X)には非可換自由群が含まれないと予想した。しかし、Margulis(1983)はそめ反例を髪=R3の場合に構成した。米ソの指導的数学者によるこの出来事は問題Aが特別な事例においても極めて難しいことを象徴するものであった。 別の例として、ローレンツ計量をもつ局所対称空間Xの場合を考えよう。このとき、xの断面曲率が正で一定という仮定の下で、基本群π1(x)は必ず有限になってしまうという現象はCalabiとMarkusによって発見された(Ann.Math.1962)。Xの普遍被覆である大域ローレンツ対称空間πでは、その等長変換からなる不連続群が極端に乏しいという意味でCalabi-Markusの現象は、この分野の将来性に対してネガティブな側面を強調する結果であった。この現象に関しては、25年後に、それがどのような状況で起こるかについて、一般の不定符号の計量をもつ簡約型等質空間G/H(特に半単純対称空間)に対して、リー群σとHの実階数条件で判定できることが証明された(小林俊行、Math.Ann.1989)。この判定条件によって、逆に、1π1(X)1=∞となるような局所等質空間が十分豊富にあるというポジティブな側面がわかったのである。 そこで、今度はどれだけ複雑な基本群が局所等質空間に起こりうるかという自然な疑問が考えられる。π1(X)が'最大'となるのはXがコンパクトのときである。コンパクト形の存在問題、言い換えれば普遍被覆空間πに余コンパクトな不連続群が存在するかどうかという問題は、やはりリーマン構造を仮定した場合には古くから研究されている。すなわち、1950年代から1960年代初頭にSiege1、Borel等によって代数群を用いた手法でコンパクトな局所リーマン対称空間の存在が証明され、さらに、双曲空間に対しては、Mostow、Gromov、Piateski-Shapiro等によって非算術的部分群も構成された。一方、非リーマン対称空間に対しては長い間、手つかずの問題であった。余コンパクトな不連続群の存在問題に対して一般的な設定での構成法(小林)と障害(obstruction)(小林一小野薫)が1980年代の後半に発見され、その後不連続群論からエルゴード理論やユニタリ表現論にまたがる手法を用いた新しい研究の潮流が国際競争の中で生まれ育っている(R.Zimmer、G.Margulis、Benoist、Oh、Witte等)。 このような現状において、本論文提出者の手塚勝貴氏は、Calabi-Markus現象と余コンパクトな不連続群の存在の中間に位置する場合に焦点を当てた。すなわち、非可換自由群やフックス群といったSL(2,R)の離散部分群やクライン群といったSL(2,C)の離散部分群がπ1(X)として実現できるかということをテーマとして問題Aに取り組んだのである。 具体的には以下の2系列の非リーマン等質空間の不連続群による商空間としてどのようなものが可能であるかを研究した。 1)Gc/Kc、Gcは複素単純リー群、(Gc,κc)は複素対称対 2)G/H、G=SL(n,R)、Hは典型的な簡約部分群 この要旨では、1)の場合のみを述べることにする。この場合、σc/κcは複素対称空間となるが、σcが単純リー群という仮定の下ではリー環レベルでは、(sl(n,C),s0(n,C))などの7つの古典型の系列と、(e6,c,f4,c)などの例外型の系列が12個に分類される(Killing,Car七an)。手塚氏の主結果は次の様に述べられる。 定理B.Gcを複素単純リー群とし、Gc/Kcを複素対称空間とする。このとき、次の4つの条件は同値である。 (i)Gcのべキ零元γ(≠e)で、それが生成する自由アーベル群くのがGc/Kcに固有不連続に作用する。 (ii)3五(2,珊が(7cへの適当な準同型を通じてGc/κcに固有に作用する。 (iii)3L(2,c)がGcへの適当な準同型写像を通じてGc/Kcに固有に作用する。 (iv)(gc,〓c)蟹(s0(P+9,C),50(P,C)(+)50(q,C))ただし、p、qは奇数で、p+gは4の倍数。 クライン群はSL(2,C)の離散部分群である。また非可換自由群はθ五(2,R)の離散部分群として実現される。定理Bから問題Aに対する以下の解答が証明された。 系C.p、qは奇数、p+qが4の倍数の時、任意のクライン群rに対し、局所複素対称空間xであって、その基本群π1(x)がrと同型であり、その普遍被覆空間が3p飢(P十9,c)/3p伽(p,C)×Spin(q,C)と同型なものが存在する。 またπ1(X)が非可換自由群になるようなxも同様に存在する。 主定理の証明は、(a)ベキ零元の標準化に関するJacobson-Morozovの定理と、(b)作用の固有性に関する小林の判定条件に加えて次の代数的な結果を用いる。 定理D.Bcを単純リー環とする。この時、次の2条件は同値となる。 (i)gcの外部自己同型写像は各ベキ零軌道を自分自身に写す。 (ii)gcは50(4n,C)と同型でない。 本論文提出者の手塚氏はDynkin-Kostant理論を用いて定理Dを証明したのであるが、定理Dのような純代数的な結果を発見し、それを局所対称空間の大域構造の定理に昇華させたアイディアは斬新で興味深い。 提出論文の第2節では変換群が3L(η,R)の場合にもベキ零軌道に関する代数的な結果をまず準備して、フックス群と同型な基本群をもつ局所等質空間がどのような場合に可能であるかについて明確で決定的な結果を得た。 このように本論文は、局所対称空間の大域構造に関して、リーマン幾何の枠組を超えた場合に意義深い新しい知見をもたらしたものであり、よって論文提出者手塚勝貴氏は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める。 | |
| UTokyo Repositoryリンク |