学位論文要旨
| No | 125578 | |
| 著者(漢字) | 山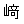 ,雅人 ,雅人 | |
| 著者(英字) | ||
| 著者(カナ) | ヤマザキ,マサヒト | |
| 標題(和) | 結晶の溶解模型と壁越え現象 | |
| 標題(洋) | Crystal Melting and Wall Crossing Phenomena | |
| 報告番号 | 125578 | |
| 報告番号 | 甲25578 | |
| 学位授与日 | 2010.03.24 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(理学) | |
| 学位記番号 | 博理第5486号 | |
| 研究科 | 理学系研究科 | |
| 専攻 | 物理学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | One of the most fundamental problems in theoretical physics in the 21st century is toconstruct a theory of quantum gravity. General relativity and quantum mechanics,which are the cornerstones of the 20st century physics, are mutually inconsistent. Weneed a theory of quantum gravity which unifies the two in a consistent framework. Over decades string theory has been the most promising candidate for quantumgravity. One of the most successful predictions of string theory, as shown by Stromingerand Vafa in 1996, is that string theory correctly reproduces the Bekenstein-Hawkingentropy of a class of supersymmetric, extremal black holes. In statistical mechanics,entropy is given by the logarithm of the number of states, and Strominger and Vafashowed that string theory reproduces the correct number of states. Their analysis hassubsequently been generalized to many other black holes. In particular, string theorynow reproduces not only the semi-classical Bekenstein-Hawking entropy of generalrelativity, but also the subleading contributions coming from the higher curvaturecorrections to the Einstein-Hilbert action. This gives a rather remarkable check ofstring theory as a theory of quantum gravity. However, there are many issues that remain to be solved. For example, the entropy istypically determined only by the asymptotic growth of the microstate degeneracies, inthe limit of charge charges. However, we hope that string theory gives a more ompleteand detailed theory of the microstates, not just their asymptotic growth. This will leadto rich and yet unknown aspects of quantum gravity. A related question is geometry at the planck scale. One of the key ideas in generalrelativity is the `"geometrization of physics", where the physics notion (e.g. mass) aretranslated and reformulated in terms of geometry (e.g. curvature). If we follow a similarpath, the central question in quantum gravity is to identify the ``quantum geometry'',geometry at the planck scale. In this thesis, we will make small steps towards these ambitious goals. Unfortunately,solving string theory in gravity backgrounds is a notoriously difficult problem. Thestrategy we take is to simplify the problem --- to replace the problem of gravity by aproblem of gauge theory. In string theory compactifications, this corresponds to takingthe Calabi-Yau manifold to be non-compact. Of course, the notion of black hole is subtlein this limit since the gravity decouples in this limit and the Newton constant becomeszero. However, part of the important data in gravity theory still remain. For example,we can still discuss entropy of black holes since we can take a scaling limit where themass of the black hole goes to infinity, thus the entropy is kept finite. The counting ofblack hole microstates is now turned into a counting problem of BPS states insupersymmetric gauge theories. The counting problem of BPS states in string theories and supersymmetric gaugetheories is an important problem, even if we forget about the motivation from black holephysics. For example, they provide primary tools to test various string dualities. BPSsolitons in supersymmetric gauge theories has a rich structure, and provides a classicexample of fruitful collaboration between physics and mathematics. Furthermore, as wewill see in later chapters there is an intimate connection with another counting problemin string theory, the topological string theory. In the first part of this thesis, we show that when X is a toric Calabi-Yau manifold(roughly meaning that X has an action of the three-dimensional torus), we can giveexplicit answers to the BPS counting problem. More precisely, each of the BPS statescontributing to the BPS index (defined in section 2.1) is in one-to-one correspondencewith a configuration of a molten crystal, and the BPS partition function ZBPS (defined insection 2.1) is the same as the statistical partition function of a crystal melting model:ZBPS=Zcrystal. Chapter 3 is devoted to the explanation of this these results. Remarkably, thederivation of the above formula depends on the newly developed mathematical theory,the non-commutative Donaldson-Thomas theory. The theory gives a new invariant forCalabi-Yau manifolds, which exactly coincides with the BPS index we are interested in.This means that BPS counting problem is important not only to physicists but also themathematicians alike. In the next chapter (chapter 4), we discuss the implication of these results toquantum gravity. We show that the thermodynamic limit of the crystal gives aprojection of the shape of the mirror of the Calabi-Yau manifold. This in particularsuggests that if we start from classical smooth geometry and approaches to the planckscale, the geometry gets discretized into a set of atoms. In this sense an atom in thecrystal melting model is an ``an atom of space'', a discretized version of the geometry atthe planck scale. We therefore see that the two problems posed earlier are now related.Each of the microstate, which is an atom of the crystal, is the discretized version of thegeometry; thus the problem of identifying black hole microstates is solved by thequantum structure of geometry! In the second half of the thesis, we move on to the discussion of the wall crossingphenomena (see section 2.2 for introduction). Wall crossing phenomena states that theBPS degeneracy jumps as we change the value of the moduli of the Calabi-Yau manifold.Wall crossing phenomena, first discussed by Cecotti and Vafa in the context ofsupersymmetric N=(2,2) theories in two dimensions, has a long history of more thannearly two decades. They also play important roles in the Seiberg-Witten theory and itsstringy realization. In these old days, it was observed that we can derive the jump ofBPS states in simple cases, but generalization seemed to be difficult. The recent breakthrough was triggered by the paper of Kontsevich and Soibelman,who proposed a rather general formula for the jumps of BPS degeneracies, generalizingthe results of Denef and Moore. Physical interpretations of the formulas weresubsequently given. In chapter 6 we discuss these formulas in detail. The wall crossing formulas can be applied to our setup, namely compactfication on thetoric Calabi-Yau manifold. In particular, the example of the resolved conifold is analyzedin Jafferi-Moore and independently in Nagao-Nakajima. There it was shown that thenon-commutative Donaldson-Thomas invariants discussed in chapter 3 is related bywall crossing to the commutative (ordinary) Donaldson-Thomas invariants. In physicslanguage, this means that the crystal melting partition function is related by wallcrossings to the topological string partition function. This clarifies the connection of ourcrystal melting model and another crystal melting model, which describes thetopological vertex. However, this is not the end of the story. First, it was observed that the BPS partitionfunction computed by the wall crossing formulas takes a beautiful infinite product form,and there should be an intuitive explanation of these results. From the viewpoint ofnon-commutative Donaldson-Thomas theory, this seems miraculous: we first computethe BPS indices separately by going through complicated mathematics, and only aftersumming up all of them and going through combinatorics can we see that the partitionfunction takes such a simple form. Moreover, it was not clear why the topological stringtheory can be related to the BPS degeneracies. Finally, as physicists we want to have anindependent way of deriving the results from purely physics arguments, without relyingon the mathematical results. This is the reason why I was motivated to give a simple derivation of the wall crossingphenomena from M-theory, which is the topic of chapter 5. By lifting type IIA braneconfigurations to M-theory and by using the 4d/5d correspondence, the problem ofcounting BPS states is mapped (under certain conditions explained in section 5) to acounting problem of free M2-brane particles in five dimensions, which span the freeparticle Fock space. This naturally explains the infinite product form of the BPSpartition function. Also, the counting problem of M2-brane particles is a generalizationof the Gopakumar-Vafa argument, which explains the appearance of the topologicalstring partition function. More precisely, we prove a formula〓The argument here is consistent with the derivations from the wall crossing formula.The bonus is that we have new mathematical predictions for non-toric examples, whichcan be tested by future mathematical developments. There is a generalization of the above-mentioned story to the case of open BPSinvariants. Closed BPS invariants discussed up to this point are defined by countingD2-branes wrapping on 2-cycles of the Calabi-Yau manifold. Open BPS invariants aredefined by counting D2-branes wrapping disks ending on another D-branes (D4-branes).Open BPS invariants are natural generalizations of closed invariants. Moreover, theygive a useful computational tool to study closed invariants for complicated geometries,as the topological vertex formaslim shows. In chapter 7 we first give a definition of the "non-commutative topological vertex",which gives a basic building block for computing open BPS invariants. The definitionuses the crystal melting model, and we perform several consistency checks of theproposal. We also discuss the wall crossing phenomena for the open BPS invariants bothwith respect to the open and closed string moduli, by again using the viewpoint ofM-theory. BPS state counting and wall crossing phenomena are still very active areas ofresearch, and has been attracting more and more attention from researchers since Istarted research. In the final chapter 8, we close this thesis by pointing out someinteresting problems which suggest directions for future research. We also collectslightly technical results in the appendices. | |
| 審査要旨 | 前世紀から引き継がれた理論物理学の最も基本的な問題の一つとして、重力理論と量子力学の融合の問題がある。弦理論はこれを解決する最も有力な候補であると考えられているが、実際すでにブラックホールの持つ熱力学的エントロピーのミクロな量子論的起源の問題に関して、注目すべき結果が得られている。すなわち、1996年、A.StromingerとC.Vafaは、ある種の超対称ブラックホールのエントロピーが弦理論の立場からミクロな状態数の対数として導出できることを示した。その後この解析は他の多くのブラックホールに対しても拡張されることがわかった。これは画期的な成果であるが、これまでの結果は、ブラックホールの持つ電荷や磁荷あるいは角運動量が大きい半古典的な場合に有効であり、真に量子的な場合の理解は課題として残っている。これは、プランクスケールにおける量子力学的な時空構造は何かという大きな問題とも関係している。 本論文は、こうした量子重力の基本的問題の解決を視野に入れながら、本質的に類似の問題である4次元の超対称ゲージ理論におけるソリトンの状態数の数え上げの問題を超弦理論の枠組みを用いて解析し、物理的にも数学的にも興味深い新しい結果を得ている。 10次元で定義される超弦理論から4次元の超対称理論を得るひとつの方法として6次元のカラビ・ヤウ多様体にコンパクト化する方法があるが、この多様体がノンコンパクトな場合には重力の自由度が分離して、N=2の超対称ゲージ理論が得られることが知られている。この理論では、超対称ブラックホールの状態数の数え上げは、ゲージ理論のソリトンの状態の数え上げに対応する。特に、1/2BPS状態と呼ばれる、超対称性を最大限保った状態の数(正確には「指数」と呼ばれる量)は量子補正を受けないので、結合定数の全領域で厳密な情報を得ることができると期待される。この量の計算は、ゲージ理論のみならず現代数学の重要な問題と密接に関係していてそれ自体興味深い。 本論文は、序論的な第1,2章、主要部分である第3章~第7章、およびまとめと展望を述べた第8章と補遺からなり、主要部分はさらに第1部(3,4章)および第2部(5,6,7章)に分けられている。 第1部では、まず第3章で、カラビ・ヤウ多様体がトーリックと呼ばれるクラスに属する場合が考察され、BPS状態の数え上げの問題が明示的に解けることが示されている。基本的なアイデアは、数え上げの問題の母関数が、3次元結晶の溶解を記述するある種の統計力学的モデルの分配関数と一致することを示し、後者を解析して厳密な答えを得るというものである。この手法自体は、簡単な場合にはすでに知られていたが、本論文では完全に一般なトーリックカラビ・ヤウ多様体に対する溶解模型を構成することにより、一般公式を得た点が新しい業績である。この公式は、数学おける非可換ドナルドソン・トーマス不変量と呼ばれる量と正確に一致しており、数学に対する貢献としても重要である。さらに第4章では、この結晶溶解模型の熱力学的極限が、もとのカラビ・ヤウ多様体のミラーと呼ばれる多様体を3次元に射影したものを与えることが示されている。この結果は、古典的な時空がプランクスケールでは結晶溶解模型のような離散的な様相を持つ可能性を示唆しているとも解釈でき、興味深い。 第2部は、第1部の結果を踏まえて、「壁越え現象」の公式の研究が展開されている。壁越え現象とは、カラビ・ヤウ多様体の形状を記述するパラメータをある「壁」を越えて動かすと、BPS状態の縮重度が突然離散的に変化する現象である。この現象について、最近KontsevichとSoibelmanにより、一般的な「壁越え公式」が提唱されたが、本論文では、まずこの公式の物理的解釈を議論し、結晶溶解に関する分配関数が壁越え現象を通じて位相的弦理論の分配関数と関係していることを明らかにした。もう一つの成果は、壁越え公式を用いるとBPS分配関数が美しい無限積の形に書かれるという数学的事実に対して、物理的で簡明な証明を与えたことである。すなわち、超弦理論における問題をもう一次元高いM理論の問題に持ち上げることにより、2サイクルに巻き付いたM2ブレーンで構成される自由な粒子のフォック空間の状態数を勘定する問題に写像し、無限積表示の簡明な導出を与えた。これは、(トーリックとは限らない)一般のカラビ・ヤウ多様体の場合を含めて適用できることから、新しい数学的結果を予言したものになっている。 以上のように、本論文にまとめられている新しい成果は、高度な数学的理論の的確な理解、およびゲージ理論及び超弦理論の深い物理的理解をもとに行われた世界的レベルの研究であり、修業年限特例にふさわしい高いレベルの博士論文であると認められる。なお、本論文の3,4章はH.Ooguri氏との共同研究に、第5章はM.Aganagic,H.Ooguri及びC.Vafa氏との共同研究に、また第7章はK.Nagao氏との共同研究に基づくが、これらの研究は論文提出者が以前から精力的に行っていたブレーンタイリングの研究と自然に繋がっており、問題設定においても技術面においても論文提出者が主体的に拘わり十分な寄与をしていると判断される。よって審査員一同博士(理学)の学位を授与できると認める。 | |
| UTokyo Repositoryリンク |