学位論文要旨
| No | 126117 | |
| 著者(漢字) | 宮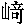 ,直 ,直 | |
| 著者(英字) | ||
| 著者(カナ) | ミヤザキ,タダシ | |
| 標題(和) | SL(3,R)の一般主系列表現の構造と関連するWhittaker関数 | |
| 標題(洋) | The structures of generalized principal series representations of SL(3,R) and related Whittaker functions | |
| 報告番号 | 126117 | |
| 報告番号 | 甲26117 | |
| 学位授与日 | 2010.03.24 | |
| 学位種別 | 課程博士 | |
| 学位種類 | 博士(数理科学) | |
| 学位記番号 | 博数理第359号 | |
| 研究科 | 数理科学研究科 | |
| 専攻 | 数理科学専攻 | |
| 論文審査委員 | ||
| 内容要旨 | 私は本論文でSL(3,R)上のWhittaker関数についての研究を行った.Whittaker関数は簡約群上の保型形式のFourier展開に現れる球関数の中で,最も基本的なものである.特にGL(n)上の保型形式に関してはPiatetski-Shapiroによって,Whittaker関数のみによるFourier展開(Fourier-Whittaker展開)が発見されており,保型L関数等への応用を考える上でWhittaker関数は非常に重要である. より明確な形で問題を述べる.Gを簡約Lie群,G=NAKをその岩澤分解とする.GのLie代数をg,その複素化をgcと表記する。極大幕単部分群Nの非退化ユニタリ指標ηに対して,Cη(∞)(N\G)をf(ng)ニη(n)f(g)((n,g)∈N×(;)をみたすようなG上の滑らかな関数f達のなす空間とし,σはこの空間に右移動で作用するものとする.σの既約許容表現(π,耳。)に対して,Iη,π=Hom(gc,K)(Hπ,K,Cη(∞)(N\G)), IG(η,π)=HomG(H∞(π),C∞(N\G))とおく.このとき,Iη,πの元の像に含まれる関数を第2種Whittaker関数と呼び,IG(η,π)の元の像に含まれる関数を第1種Whittaker関数と呼ぶ.冒頭で述べたGL(n)上の保型形式のFourier-Whittaker係数の無限素点での局所成分は第1種Whittaker関数であり,ShalikaによってZ票.は高々1次元である事が証明されている.また,G=GL(n,R)のとき,Zn,.が0でない元を持つようなπは一般主系列表現と同型になる事が知られている.本論文の目的はG=GL(3,R)またはSL(3,R)の一般主系列表現πに対して,2つの空間Zn,πと項.を明示的に理解する事である. SL(3,R)の(極小放物型部分群から誘導された)主系列表現の極小K一タイプにおけるWhittaker関数の明示式はBump[1]とManabe,Ishii,Oda[3]によって,既に与えられている.これを踏まえて研究を行い,本論文では以下の2つの結果を得た: 1.SL(3,R)の全ての一般主系列表現の(gc,K)-加群としての構造の明示的な記述を与えた. 2.SL(3,R)の極大放物型部分群から誘導された一般主系列表現の極小K-タイプにおける第1種と第2種のWhittaker関数の明示式を与えた. 本論文は独立した3つの部分に分かれている.Part1で上記の1つ目の結果について述べ,Part2,3では2つ目の結果について述べている.Part2,3の結果と既知の主系列表現の結果を合わせると,全てのGL(3,R)の一般主系列表現に対して,極小K一タイプにおけるWhittaker関数の明示式が得られた事になる.また一般主系列表現が既約なとき,原理的にはPart1での(9c,K)一加群構造の記述を用いれば,極小K一タイプにおけるWhittaker関数の明示式から,すべてのK一タイプでの明示式が得られる. Part1.The structures of standard(g,K)-modules of SL(3,R). (SL(3,R)の標準(g,K)-加群の構造) このPart1では,G=SL(3,R)のすべての一般主系列表現に対して,(9c,K)一加群構造の記述を与えた.Gの主系列表現π=IndG(P)(1N(×)eμν+ρ(×)σ)はK-加群としてL2(K)の部分空間L2(M,σ)(K)={f∈L2(K)|f(mx)=σ(m)f(x)for a.e.m∈M,x∈K}と同型になる.ここで,P=NAMは極小放物型部分群とそのLanglands分解であり,eν+ρはAの指標,σはMのユニタリ指標である.Peter-Weylの定理より,L2(M,σ)(K)はKの既約有限次元表現の行列係数からなるHilbert空間としての基底を持つ事が分かる. 以上のようにして,主系列表現のK-加群としての構造は容易に分かるため,gcの作用を記述する事が問題となる.Cartan分解g=e(×)pより,Pcの作用を記述すれば十分である.ここで,Pcの作用のK-タイプへの影響を特徴付ける線型写像を定義し,その行列表示を与えた.その結果を用いて,前述した行列係数から成る主系列表現πの基底{s(1;p,q)}l,p,q上のpcの基底{Xi}iの作用について(〓)という形の公式を得た.ここで,係数Oi(l,p,g;l',p',q')はs(l;p,q)のパラメータl,p,qの有理式で具体的に与えられている.また,極大放物型部分群から誘導された一般主系列表現についても,同様の結果を得た.このPart1の内容は論文[5]と同一である. Part2.Whittaker functions for generalized principal series representations of SL(3,R). (SL(3,R)の一般主系列表現に関するWhittaker関数) このPart2では微分方程式を解く事によって,G=SL(3,R)の極大放物型部分群から誘導された一般主系列表現の極小K-タイプにおける第1種と第2種のWhittaker関数の明示式を得た.まず,極小K-タイプ周辺の(gc,K)-加群構造を評価する事で,Whittaker関数を特徴付ける微分方程式を立式した.そして,その微分方程式を解いて,6つの幕級数解,すなわち,第2種Whittaker関数の幕級数表示を得た.また,定数倍を除いて唯一つの緩増加な解,すなわち,第1種Whittaker関数のMellin-Barnes型の積分表示(〓)を与えた.ここで,Ssiの積分路はSi:σ-〉√-1∞→σ+√-1∞(σ∈Rは被積分関数の任意の極の実部より大きくなるようにとる)であり,(ν,k)と(n1,n2,n3)はそれぞれπと極小K-タイプの基底のパラメータである.また,K-タイプを固定したとき,岩澤分解G=NAKより,Whittaker関数はそのAへの制限で特徴づけられる事に注意しておく.このPart2の内容は論文[6]と同一である. Part3.The Eisenstein series for GL(3,Z)induced from cusp forms. (尖点形式から誘導されたGL(3,Z)に関するEisenstein級数) 極小放物型Eisenstein級数と定数関数から誘導された極大放物型Eisenstein級数のFourier-Whittaker展開については,Bump[1]とFriedberg[2]によって具体的に書き下されている.このPart3では,尖点的保型表現から誘導された(;L(3,Z)に関する極大放物型Eisenstein級数のFourier-Whittaker展開を具体的に書き下した. Jacquetは主系列表現π=IndG(P)(1N(×)eν+ρ(×)σ)に対して,H∞(π)∋f→J(f;g)=SNf(wng)η(n)-1dn∈C∞(η)(N\G) (wはWeyl群の最長元)という積分(とその解析接続)で定義されるIG(η,π)の生成元を与えた.これをJacquet積分と呼ぶ.Casselmamの部分表現定理より,任意の既約許容表現は主系列表現に埋め込まれるため,任意の既約許容表現の第1種Whittaker関数がJacquet積分で与えられる.また,Jacquet積分はそのままではゼータ積分の計算等の数論的な応用に適さないものの,Eisenstein級数のFourier-Whittaker展開を書き下すのには適している.これはJacquet積分が元々,極小放物型Eisenstein級数のFourier-Whittaker係数として発見されたものである事に由来すると思われる.ここでは,まずEisenstein級数のFourier-Whittaker係数にJacquet積分を用いた表示を与え,Jacquet積分を評価する事によって,極小K一タイプにおけるMelhn-Barnes型の積分表示を得た.第1種Whittaker関数の一意性より,この積分表示は[1],[3】,Part2で得られたものと定数倍を除いて一致している.このPart3の内容は論文[4]と同一である. | |
| 審査要旨 | Whittaker関数は簡約群上の保型形式のFourier展開に現れる球関数の中で,最も基本的なものである.特にGL(n)上の保型形式に関してはPiatetski-Shapiro等によって,Whittaker関数のみによるFourier展開(Fourier-Whittaker展開)が発見されており,保型L関数等への応用を考える上でWhittaker関数は非常に基本的である. この論文において、著者は次のような結果を得た: 1.S.L(3,R)の全ての一般主系列表現の(9c,K)-加群としての構造の明示的な記述を与えた. 2.SL(3,R)の極大放物型部分群から誘導された一般主系列表現の極小K-タイプにおける第1種と第2種のWhittaker関数の明示式を与えた. 3.これの応用として、Primitiveな尖点形式から誘導されたGL(3,Z)に関するEisenstein級数のFourier展開の1次指標の対応する部分の明示的な表示式を得た. このうち、1と2の部分は、二つの論文: Tadashi Miyazaki.The structures o fstandard (g,K)-modUles of SL(3,R).Glas.Mat.Ser.Ill,43(2)=337-362,2008; Thdashi Miyazaki.Whittaker functions for generalized prinipal serie srepresentations of SL(3,R).Manuscripta Math.,128(1):107-135,2009 として既に発表されている.以下、より詳細な形で問題を述べる. Part1.SL(3,R)の標準(g,K)-加群の構造 このPart1では,G=SL(3,R)のすべての一般主系列表現に対して,(9c,K)-加群構造の記述を与えている.Gの主系列表現π=IndG(P)(1N(×)eν+ρ(×)σ)はK-加群としてL2(K)の部分空間L2(M,σ)(K)={f∈L2(K)|f(mx)=σ(m)f(x)for a.e.m∈M,x∈K}と同型になる.ここで,P=NAMは極小放物型部分群とそのLanglands分解であり,eν+ρはAの指標,σはMのユニタリ指標である,Peter-Weylの定理より,L2(M,σ)(K)はKの既約有限次元表現の行列係数からなるHilbert空間としての基底を持つ事が分かる.これで、主系列表現のK-加群としての構造は分かる.問題は,gcの作用を記述する事である. Cartan分解g=e(×)pより,Pcの作用を記述すれば十分である.ここで,Pcの作用のK-タイプへの影響を特徴付ける線型写像を定義し,その行列表示を与えた.その結果を用いて,前述した行列係数から成る主系列表現πの基底{s(l;p,q)}l,p,q上のPcの基底{Xi}iの作用について(〓)という形の公式を得た.ここで,係数Ci(l,p,q;l',p',q')はs(l;p,q)のパラメータ1,p,qの有理式で具体的に与えられている.また,極大放物型部分群から誘導された一般主系列表現についても,同様の結果を得た. Part2.SL(3,R)の一般主系列表現に関するWhittaker関数 問題の設定を少し一般的に述べる.Gを簡約Lie群,G=NAKをその岩澤分解とする.GのLie代数をg,その複素化を9cと表記する.極大幕単部分群Nの非退化ユニタリ指標ηに対して,C∞(η)(N\G)をf(ng)=η(n)f(g)((n,g)∈NxGをみたすようなG上の滑らかな関数f達のなす空間とし,Gはこの空間に右移動で作用するものとする.Gの既約許容表現(π,Hπ)に対して,Iη,π=Hom(gc,K)(Hπ,K,C∞η(N\G)), Iη,π=HomG(H∞π,C∞η(N\G))とおく.このとき,Iη.πの元の像に含まれる関数を第2種Whittaker関数と呼びIG(η.π)の元の像に含まれる関数を第1種Whittaker関数と呼ぶ.冒頭で述べたGL(n)上の保型形式のFourier-Whittaker係数の無限素点での局所成分は第1種Whittaker関数であり,ShalikaによってIη.πは高々1次元である事が証明されている.また,G=GL(n,R)のとき,Iη.πが0でない元を持っようなπは一般主系列表現と同型になる事が知られている.本論文の目的はG=GL(3,R)またはSL(3,R)の一般主系列表現πに対して,2つの空間Iη.π,TとIG(η.π)を明示的に理解する事である. SL(3,R)の(極小放物型部分群から誘導された)主系列表現の極小K-タイプにおけるWhittaker関数の明示式はclassoneのときは80年代にD.Bumpによって、その他の場合は2003年ごろH.Manabe,T.Ishii,T.Odaによって,既に与えられている. このPart2では微分方程式を解く事によって,G=SL(3,R)の極大放物型部分群から誘導された一般主系列表現の極小K-タイプにおける第1種と第2種のWhittaker関数の明示式を得た.まず,極小K-タイプ周辺の(gc,K)-加群構造を評価する事で,Whittaker関数を特徴付ける微分方程式を立式した.そして,その微分方程式を解いて,6つの幕級数解,すなわち,第2種Whittaker関数の幕級数表示を得た.また,定数倍を除いて唯一つの緩増加な解,すなわち,第1種Whittaker関数のMellin-Barnes型の積分表示を与えた. Part3.The Eisenstein series for GL(3,Z)induced from cusp forms. (尖点形式から誘導されたGL(3,Z)に関するEisen8tein級数) 極小放物型Eisenstein級数と定数関数から誘導された極大放物型Eisenstein級数のFourier-Whittaker展開については,BumpとFriedbergによって具体的に書き下されている.このPart3では,尖点的保型表現から誘導されたGL(3,Z)に関する極大放物型Eisenstein級数のFourier-Whittaker展開を具体的に書き下した.これは、Part1,2の応用になっている. 群SL(3,R)上の保型形式・保型表現に関しては、意外にも多くのことがきちんと知られていない.実のWhittaker関数に関しても、存在と一意性という,あるいみでは抽象的な結果はあるが,整数論の立場からはこれで満足するわけにはいかない.明示的な公式があることは将来のより深い研究のためには極めて有益であることは疑いがない.ここで論文の著者が得た結果は、基本的で重要である.それゆえ、論文提出者宮崎直は、博士(数理科学)の学位を受けるにふさわしい充分な資格があると認める. | |
| UTokyo Repositoryリンク | http://hdl.handle.net/2261/51757 |